The Pricing of Carbon-Linked Bonds for Agricultural Systems in Transition: Implications and Applications
May 15, 2024
PAER-2024-18
Morgan P. Mastrianni, Graduate Research Assistant; and Calum G. Turvey, Economist
1. Motivation
Recent years have witnessed a significant rise in the financing of environmentally oriented projects in the agricultural sector. Among the most salient financial products available to investors are green bonds, which are typically linked to the price of carbon or some related measure of greenhouse gas offsets. However, ‘green bond,’ and by association, green finance, is an opaque term. Most commonly, a green bond or loan offers the debtor some form of relief, usually in the form of an interest rate discount, if pre-specified conditions related to offsets are met. An example of such a condition may involve a target amount of sequestered emissions from a project funded by green bond proceeds. If the target amount is not met, bondholders may receive a lower interest rate back from the issuing company.
There are a variety of ways in which interest discounts can be managed; principal and interest payments can be reduced on amortization, with the borrower required to refund interest reductions if a goal is not met; the lender can also provide a rebate at the end of the term if conditions are satisfied and verified. However, as a matter of terminology, green bonds also include loans used for environmental remediation for which no special covenants are placed except for a statement of purpose. In many cases, a green project financed by debt will be offset by the firm by accumulating and selling carbon offsets in voluntary markets. Structuring carbon-linked bonds is complex, primarily because the stochastic properties of the underlying carbon futures prices remain largely unexamined. We offer an approach to green finance based upon a stochastic analysis of price risk in the future markets for voluntary carbon credits.
2. Carbon Futures and Bond Structures
Carbon prices can be represented in one of two ways: by the spot price, which is the current cost of one ton of carbon-equivalent emissions for immediate purchase; or by the futures price, which we will analyze with data provided by the Chicago Mercantile Exchange on recently issued carbon futures contracts. The futures price of carbon is equal to the spot price plus the cost of storing that carbon until the delivery date or maturity date. This cost is further inflated by the risk-free interest rate and the number of years to maturity. Futures prices are usually, although not always, higher than spot prices. A buyer of a futures contract hopes that the price of the underlying commodity will increase so that they can pay the seller the lower agreed-upon price and then sell the contract in the open market at its spot price, thus making a profit equal to the difference between the spot price at maturity and the contractual price. Sellers of futures contracts insure themselves against drops in commodity prices via a vice-versa process described from the buyer’s perspective.
Carbon-linked bonds could serve as a risk management tool for farmers who are interested in participating in carbon futures markets. A third party could invest in carbon futures contracts with producers, thus agreeing to provide compensation for the carbon credits generated via any change in land management practice. The price paid for credits must be at least f equal to s + c, with s being the spot price of carbon in the market and c being the cost of carry. The cost of carry refers to the cost of storing the carbon until the maturity date of the contract. This includes foregone interest that could have been earned by investing proceeds from selling the carbon at the spot price s plus any insurance or opportunity cost that the farmer might pay to store that carbon. For example, a farmer might choose not to till a tract of land if the compensated cost of carry is greater than the economic gains associated with tilling that tract and releasing the carbon. For the third-party investor to benefit economically, the spot price of carbon must increase from s by more than the cost of carry by the maturity date of the contract. In this instance, the investor may profit from selling the carbon credits at a price greater than f. This structure guards producers from downside price risk and transfers that risk to investors while providing the capital necessary to enable the adoption of on-farm practices that enhance carbon sequestration.
2.1 CME Carbon Futures
The emergence of tradable permits in the form of GEO and N-GEO futures contracts traded on the CME opens possibilities for a new line of green bonds that links amortization, coupons, or redemption directly to financing. Here, we refer to this class of structured financial products as ‘carbon-linked bonds.’ The GEO futures contracts are extraordinary in that they are linked to the average price of verified green projects’ reduced or sequestered CO2-equivalent emissions. They also offer investors the feature of transparent price discovery through tradeable forward contracts. The class of carbon-linked bonds explored in this study links the market price of carbon offsets to the coupons on term bonds. We envision a carbon-linked bond with a put option linkage that reduces the coupon payment on a pro-rata basis if the price of carbon falls.
2.2 Commodity-Linked Bonds
What if investors could voluntarily invest in bonds that, under certain predetermined conditions, give the bond issuer the right to reduce coupon payments or bond redemption values if certain conditions hold? For example, in the late 1970’s, the Government of Mexico issued a 3-year petrol-linked bond. Each 1,000-peso bond was linked to 1.95354 barrels of oil, and each bond had a coupon of 12.65823%. At maturity, the holder received either the face value of the bond or the value of the reference plus all coupons. A more recent example of a commodity-linked product is the investment-grade bond offered by Barclays Capital, which is referred to as a collateralized commodity obligation. These bonds pay regular coupons but repay the principal based on the performance of a basket of commodities, including gold, copper, and Brent crude oil. We imagine a bond similar in structure to those described above that is linked to the price of carbon, namely the futures price.
3. Monte Carlo Methods
We test whether the carbon contracts can be modeled after traditional commodities using Monte Carlo methods. The annualized drift rate and volatility are observable for both contracts. We can define a conventional commodity using the same drift rates and volatilities and model them under the assumption that the price in each period is a function of only the price from the day before, the constant drift rate, and a random shock based on the volatility of the carbon contract. This assumption is consistent with the Efficient Markets Hypothesis.
To model expected returns from bonds linked to these imagined commodities, we can generate the value of this commodity-linked bond’s coupon using the Vasicek Model for bond yields:
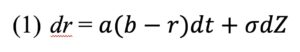
Second, we will define the commodity links by assigning a geometric Brownian motion to a commodity futures contract:
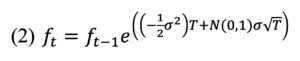
A commodity-linked bond with embedded put options will be sold at a discount to the conventional coupon. With a put option, the bond investor will share the risk of the corporation, which we presume is a marketer of the commodity, and will face reduced revenue if commodity prices fall. The coupon is given as:
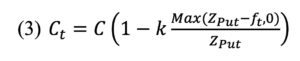
Where C is the notional coupon, k is a scale multiplier that will generally be equal to 1.0 but can be used to increase or decrease the put option’s scaled intrinsic value. The intrinsic value to the put option is Max(ZPut — ft , 0), where ZPut is the option strike price. The intrinsic value is scaled to the strike price. The bond investor shares the risk of a commodity price decrease if ZPut > ft .
Using Monte Carlo methods, we can find the expected return of a put-option bond linked to carbon contracts by simulating price paths of a commodity with the same expected drift rate and volatility as we have observed in the market and then averaging the resulting returns from each of our simulations. Our results are discussed in the following section.
4. Simulation Results
4.1 A Note on Assumptions
Our Monte Carlo simulation assumes that carbon prices follow a geometric Brownian motion. This implies that changes in price are independent from one another, and price differences across time are stationary. To justify this structure, we tested the data using a Dickey-Fuller test. To rule out the possibility of a fractional Brownian motion, we examined the Hurst coefficients from the Lo-McKinlay (2002) scaled variance ratio test as implemented for commodity futures by Turvey (2005). We found Hurst coefficients of 0.5077 for NGEO and 0.4651 for GEO. These fell within the 5% and 95% confidence intervals (0.3878 and 0.5815, respectively) of Hurst coefficients that could arise naturally from a gBm (we determined confidence intervals using Monte Carlo methods on simulated commodity price series with comparable volatility and drift rates). Combined with results from the Dickey-Fuller test, we conclude that the stochastic processes for both GEO and NGEO are consistent with a geometric Brownian motion.
We conduct a volatility sensitivity analysis of carbon-linked bonds using 10,000 Monte Carlo simulations of potential price paths. Unusually high volatilities are likely influenced by the short timeframe of our analysis. It is plausible that such high volatilities are not sustainable in competitive markets. This discrepancy is inferred from our sensitivity analysis. We analyze the expected net present values of 30-year carbon-linked bonds with variable coupon payments. Strike prices at 80%, 70%, 60%, 50%, 40%, and 30% of the price of each contract on the last day of data collection are tested for a range of volatilities. Observed volatilities are analyzed in the leftmost columns. The following columns present other possible volatilities as fractions of the observed value. Tested values are ½, ⅓, ¼, ⅕, and ⅙ of the original value.
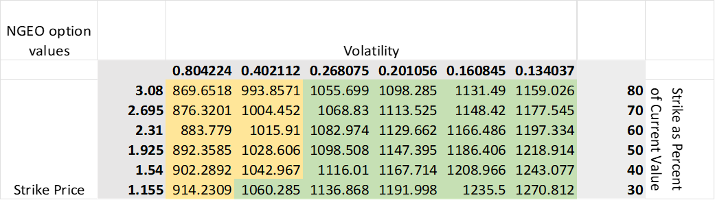
Table 1. NGEO Option Values
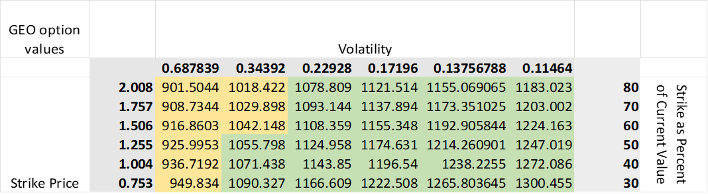
Table 2. GEO Option Values
We compare the results to the expected present value of a conventional commodity-linked bond with a face value of 1000, a coupon rate of 3.33%, and an expected interest rate of 5%. Such a bond has a slight premium in our given simulation and is valued at $1054.86. The yellow-highlighted values show where the net present value of carbon-linked bonds is less than that of the conventional commodity-linked bond. We can observe that at the realized volatilities, carbon-linked bonds are significantly discounted. This is because the price paths are much more likely to fall below each strike price tested. However, if high volatility in the market is truly unsustainable and lowers over time, then carbon-linked bonds may be priced higher than conventional bonds.
5. Discussion
A collaborative transition to sustainable agriculture has been lauded as a key step in achieving worldwide ecological and climatic goals. However, the economic case for basing our food supply chains upon principles of environmental sustainability is a less developed argument. This paper helps build the economic case for sustainable agricultural transitions by approaching the problem as a question of green finance.
We have shown that highly volatile prices in carbon markets may be a barrier to investment. When compared to conventional commodity-linked bonds, the issuer is more likely to default on (or reduce) coupon payments to investors at the current levels of market volatility. They are much less likely to default at any of our tested strike prices if volatility falls to one-third, or less, of what it was within the first year and a half of the voluntary markets opening on the CME. At these current levels, it is not more profitable to invest in carbon markets than it would be to invest in other less volatile commodities. However, if we assume that the unusually high level of volatility in carbon markets is not sustainable, then there may be significant realized profits from making long-horizon investments in carbon markets.
To demonstrate financially profitable means by which a transition to sustainable agriculture can take place, there must be a shift away from current short-termism decision frameworks common in the financial sector, which prioritize short-run returns that are often realized at the expense of long-run returns. This paper has proposed the adoption of a long-termism decision framework that prioritizes cumulative returns over a long investment horizon. One crucial barrier that must be overcome before such a shift in decision framework can take place is the ability to forecast returns over a time period that is of the proper length for our analysis. Because of this, we dedicated part of our analysis to understanding the stochastic characteristics of the underlying forces to which we link our various financial products. Given the incredibly dynamic nature of green finance and carbon markets, there is ample opportunity for future research in these markets. Key areas for further research involve investigating the variance properties of carbon markets and how closely linked to investor sentiment the price movements are. Investment professionals may consider long-term returns when designing financial products for corporate clients who are interested in participating in carbon markets that may incentivize industries such as the agricultural sector to adopt more climate-friendly management practices. With more information about the variance properties of the underlying assets, we can present a number of financial products that are of interest to parties that seek to financially incentivize carbon-smart agricultural management practices.
References
Baker, M., Bergstresser, D., Serafeim, G., & Wurgler, J. (2018). Financing the response to climate change: the pricing and ownership of U.S. green bonds. Social Science Research Network. https://doi.org/10.2139/ssrn.3275327
Cannon, M. J., Percival, D. B., Caccia, D. C., Raymond, G. M., & Bassingthwaighte, J. B. (1997). Evaluating scaled windowed variance methods for estimating the Hurst coefficient of time series. Physica. A, 241(3–4), 606–626. https://doi.org/10.1016/s0378-4371(97)00252-5
Carr, P. (1987). A note on the pricing of Commodity-Linked bonds. The Journal of Finance, 42(4), 1071–1076. https://doi.org/10.1111/j.1540-6261.1987.tb03928.x
Climate-Smart Agriculture. (N.D.) World Bank. Retrieved February 27, 2023, from https://www.worldbank.org/en/topic/climate-smart-agriculture
Graves, T., Gramacy, R. B., Watkins, N. W., & Franzke, C. (2017). A brief history of long memory: Hurst, Mandelbrot and the Road to ARFIMA, 1951–1980. Entropy, 19(9), 437. https://doi.org/10.3390/e19090437
Koutsoyiannis, D. (2003). Climate change, the Hurst phenomenon, and hydrological statistics. Hydrological Sciences Journal, 48(1), 3–24. https://doi.org/10.1623/hysj.48.1.3.43481
Lebowitz, J. L., & Penrose, O. (1973). Modern ergodic theory. Physics Today, 26(2), 23–29. https://doi.org/10.1063/1.3127948
Liu, S. (2022). On the ergodic properties of climate change with implications for agricultural resilience and sustainability. [Master’s Thesis, Cornell University]. https://ecommons.cornell.edu/items/a768a85b-deb4-44d0-8291-ad6b1ff366cf
Mandelbrot, B. B., & Wallis, J. R. (1969). Robustness of the rescaled range R/S in the measurement of noncyclic long run statistical dependence. Water Resources Research, 5(5), 967–988. https://doi.org/10.1029/wr005i005p00967
Munshi, J. (2015). The hurst exponent of surface temperature: a note. Social Science Research Network. https://doi.org/10.2139/ssrn.2689425
Paulson Institute. (2020). Financing Nature: Closing the Global Biodiversity Financing Gap. https://www.paulsoninstitute.org/CONSERVATION/FINANCING-NATURE-REPORT/
Stephenson, D. B., Collins, M., Rougier, J., & Chandler, R. E. (2012). Statistical problems in the probabilistic prediction of climate change. Environmetrics, 23(5), 364–372. https://doi.org/10.1002/env.2153
The Paris Agreement | UNFCCC. (n.d.). Retrieved February 27, 2023 from https://unfccc.int/process-and-meetings/the-paris-agreement
Turvey, C. G. (2006). Managing food industry business and financial risks with commodity-linked credit instruments. Agribusiness, 22(4), 523–545. https://doi.org/10.1002/agr.20102
Turvey, C. G. (2005). The pricing of degree-day weather options. Agricultural Finance Review, 65(1), 59–85. https://doi.org/10.1108/00214660580001167
Turvey, C. G. (2007). A note on scaled variance ratio estimation of the Hurst exponent with application to agricultural commodity prices. Physica. A, 377(1), 155–165. https://doi.org/10.1016/j.physa.2006.11.022
Turvey, C. G., & Wang, Y. (2012). The Effects of Government Sponsored Enterprise (GSE) Status on the Pricing of Bonds Issued by the Federal Farm Credit Banks Funding Corporation (FFCB). Agricultural Finance Review 72(3): 488–506. https://doi.org/10.1108/00021461211277303
Turvey, C. G., & Wongsasutthikul, P. (2016). An autoregressive approach to modeling commodity prices as a quasi-fractional Brownian motion. Agricultural Finance Review, 76(1), 54–75. https://doi.org/10.1108/afr-01-2016-0004
Uranga, Josefina. (2023). Carbon. It Ain’t No. 2 Yellow Corn. [Master’s Thesis, Cornell University].
The World Bank. (2022). State and Trends of Carbon Pricing 2022 [Serial]. The World Bank. http://documents.worldbank.org/curated/en/099045006072224607/P1780300092e910590acb201757ecd54322
Zhu, Z., & Taqqu, M. S. (2006). Impact of the sampling rate on the estimation of the parameters of fractional Brownian motion. Journal of Time Series Analysis, 27(3), 367–380. https://doi.org/10.1111/j.1467-9892.2005.00470.x
