Management of captive populations

Captive breeding programs have been established to maintain population-wide genetic diversity and fitness, at least until reintroductions or supplementation of wild populations occur. Often, the goal is to retain at least 90% of the initial diversity for 200 years. This is accomplished by limiting selection and reducing the loss of alleles due to inbreeding and drift. One method of reducing the impact of drift through breeding is a procedure for minimizing mean kinship when choosing breeders from the population. Selecting breeders by minimizing mean kinship equalizes the proportion of genes that are identical by descent. This means that individuals likely to harbor rare alleles will be selected to breed over individuals that are likely to have alleles that are more common in the population. By continually selecting individuals with rare alleles, the likelihood of losing the alleles is decreased, leading to the retention of genetic diversity across generations of captive breeding.
To manage a population using a minimizing mean kinship approach, the kinship for all pairwise individuals is first calculated. Next, these values are used to calculate the average kinship for each individual and then these values are ranked for all individuals. Finally, the individual with the highest mean kinship is removed from the pool of potential breeders, since this individual likely has the least unique (most common) alleles in the population. After removal, the pairwise mean kinships are recalculated and another individual removed from the list of potential breeders until no individuals remain. The last male and female removed from the list become an assigned pair. This process can be represented mathematically. To start, the kinship of a single individual is calculated by Fi = Σ½n(1 + FA)
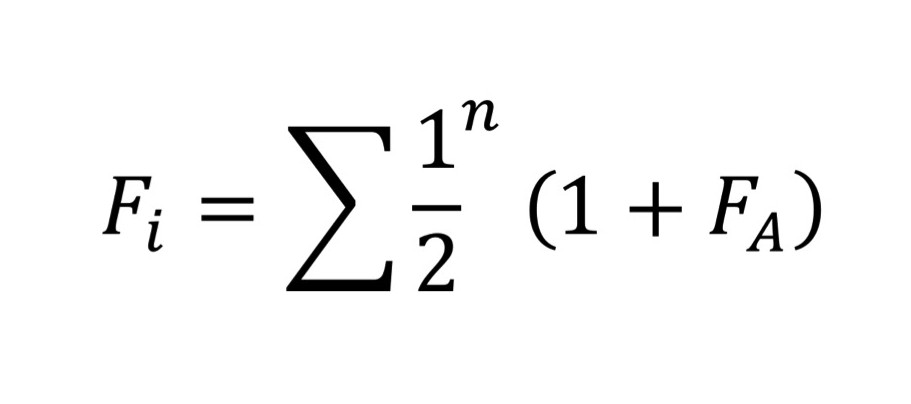
where n is the number of individuals in individual i’s pedigree history, and FA describes the relationship of the founding population. Thus, Fi is a quantification of inbreeding within individual i. Next, mean kinship is calculated using the kinship coefficient between a pair of potential parents ∫ij = Fi + Fj
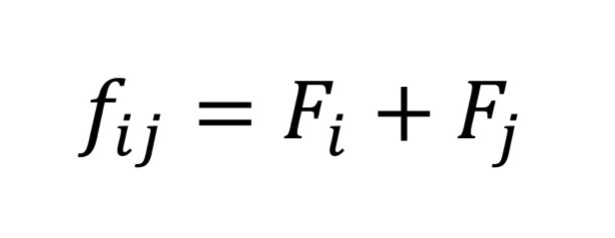
where Fi and Fj are the inbreeding coefficients calculated from the pedigree for individuals i and j, since the inbreeding coefficient in any individual is the sum of the inbreeding coefficients of the parents. Using fij the mean kinship of individual i is equal to the average inbreeding of individual i to the population and is calculated by
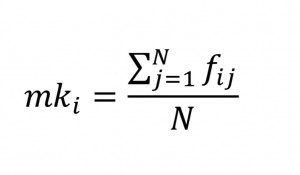
where N is the number of individuals in the population (Ballou and Lacy 1995).
This method – called ranked mean kinship – works well for species that can be held at discrete generations because the selection of breeders directly determines the diversity of the next generation via the breeders’ offspring. This is not true of populations with overlapping generations because, if both parents and offspring contribute to the diversity contained within the next generation, controlling the diversity in the offspring only does not minimize relatedness (or maximize diversity retained) in the population as a whole, especially when the number of adults is much large than the number of offspring.
